常微分方程

首先需要回忆高数上的微分方程。有了这样的概念后，我们就能愉快地连续化神经网络层级，并构建完整的神经常微分方程。

常微分方程即只包含单个自变量 x、未知函数 f(x) 和未知函数的导数 f’(x) 的等式，所以说 f’(x) = 2x 也算一个常微分方程。 但更常见的可以表示为 $df(x)/dx = g(f(x), x)$ ,其中 $g(f(x), x)$ 表示由 f(x) 和 x 组成的某个表达式 对于这个常微分方程，需要解出 f(x) , 但是工程上只需要数值解：即给定一个初值 f(x_0)，我们希望解出末值 f(x_1)，这样并不需要解出完整的 f(x)，只需要一步步逼近它就行了

神经网络，本质上不论是全连接、循环还是卷积网络，它们都类似于一个非常复杂的复合函数，复合的次数就等于层级的深度。例如两层全连接网络可以表示为 $Y=f(f(X, θ1), θ2)$

普通神经网络适用复合函数的求导方法。前向传播过后需要保留所有层的激活值，并在沿计算路径反传梯度时利用这些激活值。这对内存的占用非常大。神经常微分方程使用神经网络参数化隐藏状态的导数，参数也是一个连续的空间，我们不需要再分层传播梯度与更新参数。经微分方程在前向传播过程中不储存任何中间结果，因此它只需要近似常数级的内存成本。

如何理解 使用神经网络参数化隐藏状态的导数？

从残差网络到微分方程

考虑残差神经网络

$$ h _{t+1} = h_ t + f(h_t,\theta{_t})$$$$ dh(t)/dt = f(h(t), t,\theta)$$

现在若能得出该常微分方程的数值解，那么就相当于完成了前向传播。

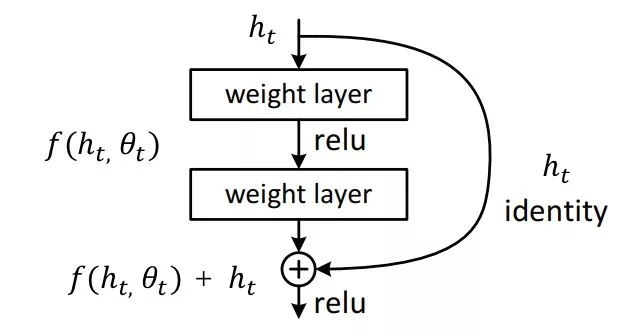
$$ \frac{d h ( t )} {d t}=f ( h ( t ), t, \theta) $$$$\int_{t_{0}}^{t_{1}} d h ( t )=\int_{t_{0}}^{t_{1}} f ( h ( t ), t, \theta) d t $$$$h ( t_{1} )=h ( t_{0} )+\int_{t_{0}}^{t_{1}} f ( h ( t ), t, \theta) d t $$

如上所示，常微分方程的数值解 $h(t_1)$ 需要求神经网络 f 从 $t_0$ 到 $t_1$ 的积分。我们完全可以利用 ODE solver 解出这个值，这在数学物理领域已经有非常成熟的解法，我们只需要将其当作一个黑盒工具使用就行了。

连续型的归一化流

流生成模型

基于流的生成模型 - 维基百科，自由的百科全书 一种使用 概率密度 变量变换法将简单分布转换为复杂分布的统计方法。

$$\int p(x)dx=\int\pi(z)dz=1\text{ ; Definition of probability distribution.} $$$$p(x)=\pi(z)\left|\frac{dz}{dx}\right|=\pi(f^{-1}(x))\left|\frac{df^{-1}}{dx}\right|=\pi(f^{-1}(x))|(f^{-1})^{\prime}(x)| $$

导数的绝对值 用于确保概率密度非负，并反映变量变换时的“伸缩比例”。 直观解释

  • 若变换 f 将 z 拉伸（例如放大 2 倍），则 x 的密度会稀释为原来的 1/2。
  • 若变换压缩 z（例如缩小为 1/2），则 x 的密度会加倍。
$$\mathbf{z}\sim\pi(\mathbf{z}),\mathbf{x}=f(\mathbf{z}),\mathbf{z}=f^{-1}(\mathbf{x})$$$$p(\mathbf{x})=\pi(\mathbf{z})\left|\det\frac{d\mathbf{z}}{d\mathbf{x}}\right|=\pi(f^{-1}(\mathbf{x}))\left|\det\frac{df^{-1}}{d\mathbf{x}}\right|$$
  • det 表示雅可比矩阵的行列式，衡量多维空间中的体积缩放因子。 $p(x)$ 表示在通过函数 x=f(z) 将随机变量 z 从其原始空间变换到新的空间后，新变量 x 的概率密度分布。 取对数，得到 z 的对数似然为：

似然函数为由因求果。似然函数就是给定参数下，z 的概率密度，取 log 则为对数似然。

$$ \operatorname{l o g} p_{K} ( z_{K} )=\operatorname{l o g} p_{0} ( z_{0} )-\sum_{i=1}^{K} \operatorname{l o g} \left| \operatorname* {d e t} \frac{d f_{i} ( z_{i-1} )} {d z_{i-1}} \right| $$
  • 雅可比行列式的意义：行列式 $\operatorname* {d e t} \frac{d f_{i} ( z_{i-1} )} {d z_{i-1}}$ 衡量了变换 $f_i$ 对空间的局部体积缩放比例。
    • 若行列式绝对值 > 1，变换拉伸空间，概率密度被稀释，需减少密度值。
    • 若行列式绝对值 < 1，变换压缩空间，概率密度被集中，需增加密度值。

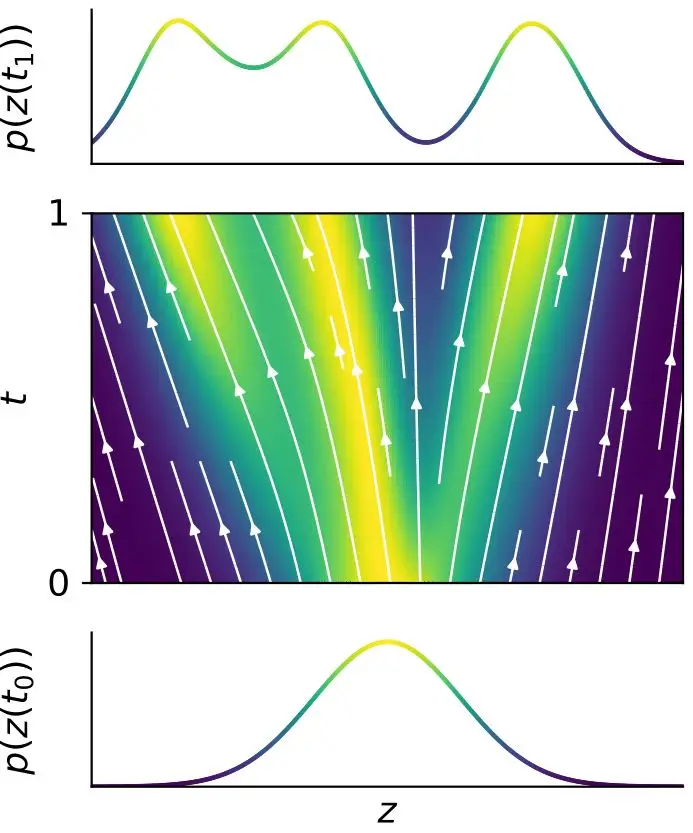
连续型归一化流

$$ \operatorname{l o g} q ( \mathbf{Z} ( t_{1} ) | X, \mathbf{A} )=\operatorname{l o g} q ( \mathbf{Z} ( t_{0} ) | X, \mathbf{A} )-\int_{t_{0}}^{t_{1}} \mathrm{T r} \left( {\frac{\partial f} {\partial\mathbf{Z} ( t )}} \right) d t \tag{11} $$

在模型训练时，需要最大化 所求目标分布的 对数似然，让生成的样本更接近真实数据

随机变量 $z(t _0)$ 及其分布可以通过一个连续的转换演化到 $z(t_ 1)$ 及其分布： |430

Reference