问题定义

变分推断（Variational Inference, VI）是 贝叶斯近似推断 方法中的一大类方法，将后验推断问题巧妙地转化为优化问题进行求解。

全称为：证据下界 Evidence Lower Bound

ELBO 实际上是从 KL 散度和条件概率公式推断出来的，并不涉及复杂数学操作。 本质上是 要求一个后验分布，但是后验分布不好求，则求一个最优的替代分布。使用 KL 散度衡量替代分布和真实分布的距离，最小化这个距离，去除无关项则得到 ELBO 公式。

给定 observation variable x （比如 RGB 图片）和 latent variable z （比如是 RGB 图片经过 encoder 得到的 latent feature）, 假设我们想知道（学习）后验概率 $p(z|x)$ ，但发现 $p(z|x)$ 在实际中不好或者没法求解，那么我们该怎么求解这个后验概率呢？

推导

概率分布的表示

|490

$$q^*(\boldsymbol{z})=\underset{q(\boldsymbol{z})\in Q}{\operatorname*{\arg\min}}L\left(q(\boldsymbol{z}),p(\boldsymbol{z}|\boldsymbol{x})\right)$$

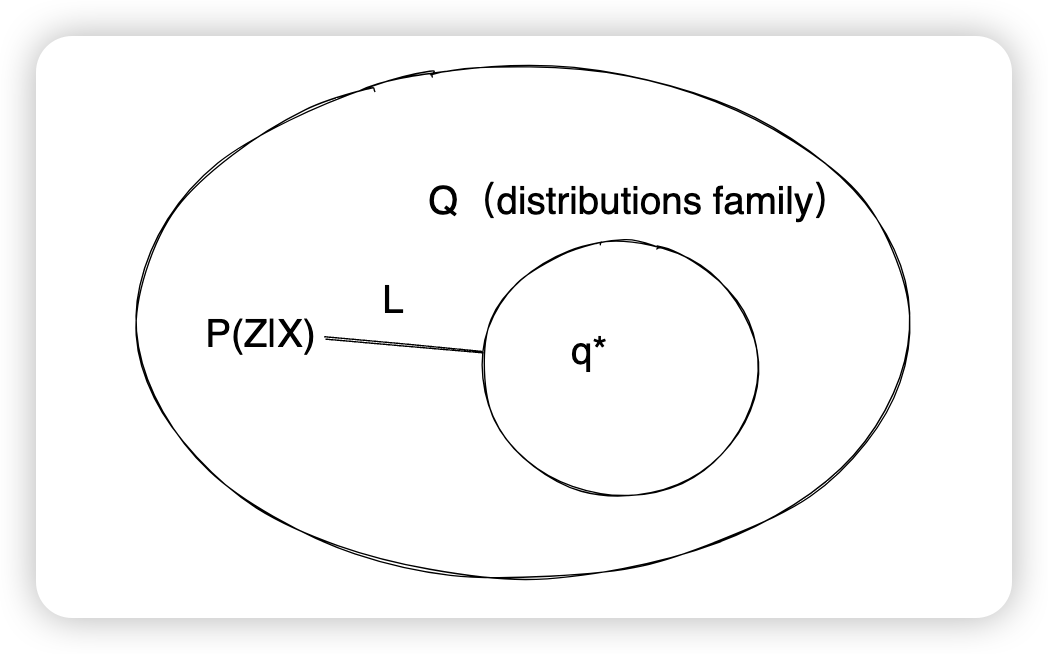
需要明确的是： $p(z|x)$ 是 后验分布，表示 参数 z 在观察到 数据 x 后的概率分布，x->z $q(z)$ 是 一个普通概率分布 使用 $q$ 做区分 实际要求的是 $p(z|x)$，但是不好求，所以需要找一个最优 $q(z)$ ，也就是 $q^*(z)$

ELBO 推导

$$L(q(z),p(z|x))=\mathrm{KL}(q(z)||p(z|x))$$$$\begin{aligned} q^{*}(z) & =\arg\min_{q(\boldsymbol{z})\in Q}\mathsf{KL}\left(q(\boldsymbol{z})||p(\boldsymbol{z}|\boldsymbol{x})\right) \\ & =\arg\min_{q(\boldsymbol{z})\in Q}-\int_{\boldsymbol{z}}q(\boldsymbol{z})\log\left[\frac{p(\boldsymbol{z}\mid\boldsymbol{x})}{q(\boldsymbol{z})\boldsymbol{z}}\right]d\boldsymbol{z} \end{aligned}$$

由于 KL 散度大于等于 0，如果不限制 $q*$ 的分布，那么最好的情况就是让$q^{*}(z)=p(z|x)$。 但是当 $q*$ 的分布 属于 Q 就不一定了

$$\begin{aligned} \mathsf{KL}(q(z)||p(z\mid x)) & =-\int_{z}q(\boldsymbol{z})\log\left[\frac{p(\boldsymbol{z}\mid\boldsymbol{x})}{q(\boldsymbol{z})}\right]d\boldsymbol{z} \\ & =\int_{\boldsymbol{z}}q(\boldsymbol{z})\log q(\boldsymbol{z})d\boldsymbol{z}-\int_{\boldsymbol{z}}q(\boldsymbol{z})\log p(\boldsymbol{z}|\boldsymbol{x})d\boldsymbol{x} \end{aligned}$$

这里关于 q(z) 对z积分，其实就是关于 q(z) 的期望，即 $\int_{z}^{}q(z)f(z,\cdot)dz =\mathbb{E}_q[f(z,\cdot)]$ ,那么上式能表示成期望形式：

连续型随机变量的期望公式：$\mathbb{E}[Z] = \int_{-\infty}^{\infty} z \cdot q(z) dz$ 函数随机变量的期望公式：$\mathbb{E}[f(Z)] = \int_{-\infty}^{\infty} f(z) \cdot q(z) dz$

$$\begin{aligned} \mathsf{KL}(q(\boldsymbol{z})||p(\boldsymbol{z}\mid\boldsymbol{x})) & =-\int_{z}q(\boldsymbol{z})\log\left[\frac{p(\boldsymbol{z}\mid\boldsymbol{x})}{q(\boldsymbol{z})}\right]d\boldsymbol{z} \\ & =\int_\boldsymbol{z}q(\boldsymbol{z})\log q(\boldsymbol{z})d\boldsymbol{z}-\int_\boldsymbol{z}q(\boldsymbol{z})\log p(\boldsymbol{z}\mid\boldsymbol{x})d\boldsymbol{z} \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q[\log p(\boldsymbol{z}\mid\boldsymbol{x})] \end{aligned}$$$$\begin{aligned} \mathsf{KL}(q(\boldsymbol{z})||p(\boldsymbol{z}\mid\boldsymbol{x})) & =-\int_{z}q(z)\log\left[\frac{p(z\mid x)}{q(z)}\right]dz \\ & =\int_\boldsymbol{z}q(\boldsymbol{z})\log q(\boldsymbol{z})d\boldsymbol{z}-\int_\boldsymbol{z}q(\boldsymbol{z})\log p(\boldsymbol{z}\mid\boldsymbol{x})d\boldsymbol{z} \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q[\log p(\boldsymbol{z}\mid\boldsymbol{x})] \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q\left[\log\left[\frac{p(\boldsymbol{x},\boldsymbol{z})}{p(\boldsymbol{x})}\right]\right] \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q[\log p(\boldsymbol{x},\boldsymbol{z})]+\mathbb{E}_q[\log p(\boldsymbol{x})] \end{aligned}$$$$\begin{aligned} \mathsf{KL}(q(\boldsymbol{z})||p(\boldsymbol{z}\mid\boldsymbol{x})) & =-\int_{z}q(\boldsymbol{z})\log\left[\frac{p(\boldsymbol{z}\mid\boldsymbol{x})}{q(\boldsymbol{z})}\right]d\boldsymbol{z} \\ & =\int_\boldsymbol{z}q(\boldsymbol{z})\log q(\boldsymbol{z})d\boldsymbol{z}-\int_\boldsymbol{z}q(\boldsymbol{z})\log p(\boldsymbol{z}\mid\boldsymbol{x})d\boldsymbol{z} \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q[\log p(\boldsymbol{z}\mid\boldsymbol{x})] \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q\left[\log\left[\frac{p(\boldsymbol{x},\boldsymbol{z})}{p(\boldsymbol{x})}\right]\right] \\ & =\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q[\log p(x,\boldsymbol{z})]+\mathbb{E}_q[\log p(\boldsymbol{x})] \\ & =\underbrace{\mathbb{E}_q[\log q(\boldsymbol{z})]-\mathbb{E}_q[\log p(\boldsymbol{x},\boldsymbol{z})]}_{-\mathrm{ELBO}}+\log p(\boldsymbol{x}) \end{aligned}$$

此时，我们把前两项称之为 -ELBO (Evidence Lower Bound)。（注意这里是负的ELBO） 要最小化 KL 散度，只要最大化 ELBO 即可。 公式表示为

$$\begin{aligned} q^{*}(\boldsymbol{z}) & =\underset{q(\boldsymbol{z})\in Q}{\operatorname*{\operatorname*{argmin}}}\mathsf{KL}(q(\boldsymbol{z})||\overbrace{p(\boldsymbol{z}\mid\boldsymbol{x})}^{\mathrm{unknown}}) \\ & =\underset{q(\boldsymbol{z})\in Q}{\operatorname*{\operatorname*{argmax}}}\mathsf{ELBO}(q) \end{aligned}$$

ELBO计算

$$\mathsf{ELBO}(q)=\mathbb{E}_q\left[\log p(x,z)\right]-\mathbb{E}_q\left[\log q(z)\right]$$

实际计算中，ELBO 可以表示成以下形式进行计算,使用任一形式均可：

$$\begin{align*}ELBO(q) &= \mathbb{E}_q[\log{p(x,z)}]-\mathbb{E}_q[\log{q(z)}]\\ &= \mathbb{E}_q[\log{p(x|z)p(z)}]-\mathbb{E}_q[\log{q(z)}]\\ &= \mathbb{E}_q[\log{p(x|z)}]+\mathbb{E}_q[\log{p(z)}]-\mathbb{E}_q[\log{q(z)}]\\ &= \mathbb{E}_q[\log{p(x|z)}]+\mathbb{E}_q[\frac{\log{p(z)}}{\log{q(z)}}]\\ &= \mathbb{E}_q[\log{p(x|z)}]+\int_{z}^{}q(z)\frac{\log{p(z)}}{\log{q(z)}}dz\\ &= \mathbb{E}_q[\log{p(x|z)}]-KL(q(z)||p(z)) \end{align*}$$

此时 ELBO 已经推导完毕。

$$\begin{aligned} \log p(\boldsymbol{x}) & =\mathsf{ELBO}(q)+\mathsf{KL}\left(q(\boldsymbol{z})||p(\boldsymbol{z}|\boldsymbol{x})\right) \\ & \geq\mathsf{ELBO}(q) \end{aligned}$$

ELBO其实就是数据Evidence $\log{p(x)}$ 的下界。

Reference